Using CUDA to Accelerate the Algorithms to Find the Maximum Value in a Range with CPU and GPU

Nowadays, we have to deal with massive amounts of data, so the speed of calculations is critical. Traditional CPU technology is no longer capable of meeting computational demand. Parallel computing allows us to solve this problem by using multiple computing resources simultaneously. This technology is based on the capability of the GPU to divide computing tasks into hundreds of smaller ones and run them concurrently. However, to achieve a drastic increase in computing performance, developers have to rethink their algorithms to make them parallel.

In one of our previous posts, we provided tips on using CUDA, NVIDIA’s parallel computing architecture that harnesses the power of the GPU and CPU. CUDA allows developers to parallelize and accelerate computations across separate threads on the GPU simultaneously. The CUDA architecture is widely used for many purposes: linear algebra, signal processing, image and video processing, and more. How to optimize your code to reveal the full potential of CUDA is the question we’ll investigate.

In this article, we want to share our experience using CUDA for defining the fastest way to find the max element and its index with different algorithms, comparing to std::max_element in C++. This article might be useful for developers who are looking for the fastest way to perform computations.

To better understand the capabilities of CUDA for speeding up computations, we conducted tests to compare different ways of optimizing code to find the maximum absolute value of an element in a range and its index.

We ran our tests on both the CPU and GPU using different methods of code optimization. During the CPU tests, we applied three different policies for parallel and sequential execution. When we carried out our tests on the GPU, we used a non-optimized method of algorithm execution as well as five algorithms optimized for the parallel architecture.

We conducted our tests using the following hardware and software:

• Intel Core i5-4460, 16GB RAM
• NVIDIA GeForce GTX 1060 6GB
• СUDA 10
• Visual Studio 2017

Using other hardware or a different CUDA version wouldn’t have made a significant difference.

As input data, we took a range of 250,000 float elements. We ran the search 1,000 times.

You can find the full source code of our testing project here: cuda-reduce-max-with-index.

Let’s take a look at our tests first and then compare the results.

Searching on the CPU

For conducting our tests, we took the max_element() algorithm from the C++ standard library, which finds the maximum value in a range and runs on the CPU. We tested three options for executing this algorithm according to the execution policy that appeared in C++17 for parallel and sequential algorithm execution:

1. Sequenced_policy (execution::seq) makes the algorithm execute sequentially without parallelism in the calling thread.
2. Parallel_policy (execution::par) allows the parallel algorithm functions to execute in either the invoking thread or a thread implicitly created by the library. Any such invocations are indeterminately sequenced with respect to each other.
3. Parallel_unsequenced_policy makes the parallel algorithm execute in an unordered but parallel fashion in unspecified threads implicitly created by the library.

Here’s how we did this:

template <class ExPol >
void cpuMaxIdx(ExPol pol, const vector <float >& input, float* max_out, int* max_idx_out)
{
    auto maxIt = max_element(pol, begin(input), end(input), [](float a, float b) { return fabs(a) < fabs(b); });
    *max_out = *maxIt;
    *max_idx_out = maxIt - begin(input);
}

Searching on the GPU

We also ran six algorithms searching for the maximum value in a range on the GPU in ways both non-optimized and optimized for parallel execution:

Non-optimized algorithm on GPU

This algorithm works as a standard sequential search loop that looks for the maximum value and its index.

__global__ void reduceMaxIdx(const float* __restrict__ input, const int size, float* maxOut, int* maxIdxOut)
{
    float max = 0.0;
    int maxIdx = 0;
  
    for(int i = 0; i < size; i++)
    {
        if (fabs(input[i]) > max)
        {
            max = fabs(input[i]);
            maxIdx = i;
        }
    }
  
    maxOut[0] = max;
    maxIdxOut[0] = maxIdx;
}

Optimized GPU thread with local memory

In this case, we optimized the loop for parallel execution in multiple threads. Each thread saves the maximum value and its index in local memory during loop execution.

Here’s what the optimized GPU thread looks like:

global__ void reduceMaxIdxOptimized(const float* __restrict__ input, const int size, float* maxOut, int* maxIdxOut)
{
    float localMax = 0.f;
    int localMaxIdx = 0;
  
    for (int i = threadIdx.x; i < size; i += blockDim.x)
    {
        float val = input[i];
  
        if (localMax < abs(val))
        {
            localMax = abs(val);
            localMaxIdx = i;
        }
    }
  
    atomicMax(maxOut, localMax);
  
    __syncthreads();
  
    if (*maxOut == localMax)
    {
        *maxIdxOut = localMaxIdx;
    }
}

The absolute maximum is saved to the max_out parameter using the atomicMax operation, which is separately realized for floating-point numbers, as CUDA supports this operation only for whole numbers.

The index is defined by checking if the local maximum is absolute.

__device__ void atomicMax(float* const address, const float value)
{
    if (*address >= value)
    {
        return;
    }
  
    int* const addressAsI = (int*)address;
    int old = *addressAsI, assumed;
  
    do
    {
        assumed = old;
        if (__int_as_float(assumed) >= value)
        {
            break;
        }
  
        old = atomicCAS(addressAsI, assumed, __float_as_int(value));
    } while (assumed != old);
}

Optimized GPU thread with shared memory

The following algorithm represents a more complex variation of the previous. In this case, the atomicMax operation deals with the memory – shared by all threads in a block and offering high access speed – to which the maximum values for all threads in that block are written.

__global__ void reduceMaxIdxOptimizedShared(const float* __restrict__ input, const int size, float* maxOut, int* maxIdxOut)
{
    __shared__ float sharedMax;
    __shared__ int sharedMaxIdx;
  
    if (0 == threadIdx.x)
    {
        sharedMax = 0.f;
        sharedMaxIdx = 0;
    }
  
    __syncthreads();
  
    float localMax = 0.f;
    int localMaxIdx = 0;
  
    for (int i = threadIdx.x; i < size; i += blockDim.x)
    {
        float val = input[i];
  
        if (localMax < abs(val))
        {
            localMax = abs(val);
            localMaxIdx = i;
        }
    }
  
    atomicMax(&sharedMax, localMax);
  
    __syncthreads();
  
    if (sharedMax == localMax)
    {
        sharedMaxIdx = localMaxIdx;
    }
  
    __syncthreads();
  
    if (0 == threadIdx.x)
    {
        *maxOut = sharedMax;
        *maxIdxOut = sharedMaxIdx;
    }
}

Optimized GPU thread blocks

This algorithm to search for the maximum value was modified for additional parallelization of CUDA thread blocks. The loop is built taking into account the parallel execution of blocks. While the shared memory is only available within one block, the atomicMax function will return not the maximum value and its index but a range of values, one from each block used. The absolute maximum value will be selected from the range received as an output.

__global__ void reduceMaxIdxOptimizedBlocks(const float* __restrict__ input, const int size, float* maxOut, int* maxIdxOut)
{
    __shared__ float sharedMax;
    __shared__ int sharedMaxIdx;
  
    if (0 == threadIdx.x)
    {
        sharedMax = 0.f;
        sharedMaxIdx = 0;
    }
  
    __syncthreads();
  
    float localMax = 0.f;
    int localMaxIdx = 0;
  
    for (int i = threadIdx.x + blockIdx.x * blockDim.x; i < size; i += blockDim.x)
    {
        float val = input[i];
  
        if (localMax < abs(val))
        {
            localMax = abs(val);
            localMaxIdx = i;
        }
    }
  
    atomicMax(&sharedMax, localMax);
  
    __syncthreads();
  
    if (sharedMax == localMax)
    {
        sharedMaxIdx = localMaxIdx;
    }
  
    __syncthreads();
  
    if (0 == threadIdx.x)
    {
        maxOut[blockIdx.x] = sharedMax;
        maxIdxOut[blockIdx.x] = sharedMaxIdx;
    }
}

Warp optimized GPU with local and shared memory

This algorithm was performed using synchronized data exchange between threads within a warp (which contains 32 threads) to reduce the number of atomic operations in CUDA.  

 

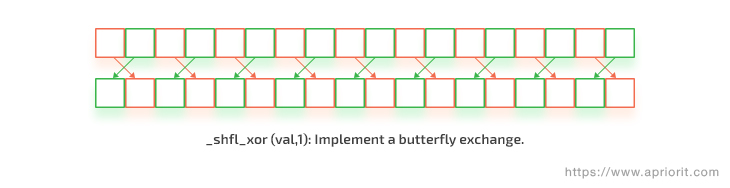
Figure 1. Synchronized data exchange example inside a warp

Similar to the previous case, the algorithm is executed in two stages:

• Search for the maximum value in each thread and write it to local memory
• Search for the maximum value and its index inside the warp using data exchange

Let’s look at the source code for the first stage:

__global__ void reduceMaxIdxOptimizedWarp(const float* __restrict__ input, const int size, float* maxOut, int* maxIdxOut)
{
    float localMax = 0.f;
    int localMaxIdx = 0;
  
    for (int i = threadIdx.x; i < size; i += blockDim.x)
    {
        float val = input[i];
  
        if (localMax < abs(val))
        {
            localMax = abs(val);
            localMaxIdx = i;
        }
    }
  
    const float warpMax = warpReduceMax(localMax);
  
    const int warpMaxIdx = warpBroadcast(localMaxIdx, warpMax == localMax);
  
    const int lane = threadIdx.x % warpSize;
  
    if (lane == 0)
    {
        int warpIdx = threadIdx.x / warpSize;
        maxOut[warpIdx] = warpMax;
        maxIdxOut[warpIdx] = warpMaxIdx;
    }
}

Here, we used the __shfl_xor_sync operation for finding the maximum value within the warp and the __ballot_sync and __shfl_sync operations for finding the index.

__inline__ __device__ float warpReduceMax(float val)
{
    const unsigned int FULL_MASK = 0xffffffff;
  
    for (int mask = warpSize / 2; mask > 0; mask /= 2)
    {
        val = max(__shfl_xor_sync(FULL_MASK, val, mask), val);
    }
      
    return val;
}
  
template <class T >
__inline__ __device__ float warpBroadcast(T val, int predicate)
{
    const unsigned int FULL_MASK = 0xffffffff;
  
    unsigned int mask = __ballot_sync(FULL_MASK, predicate);
  
    int lane = 0;
    for (;!(mask & 1); ++lane)
    {
        mask > >= 1;
    }
      
    return __shfl_sync(FULL_MASK, val, lane);
}

This algorithm can be executed with or without shared memory. In the latter case, the results are written directly to the output parameters of the atomicMax function.

Analyzing the results

We calculated the speed of execution for each algorithm with the selected input data and compared the results in the following diagram:

 

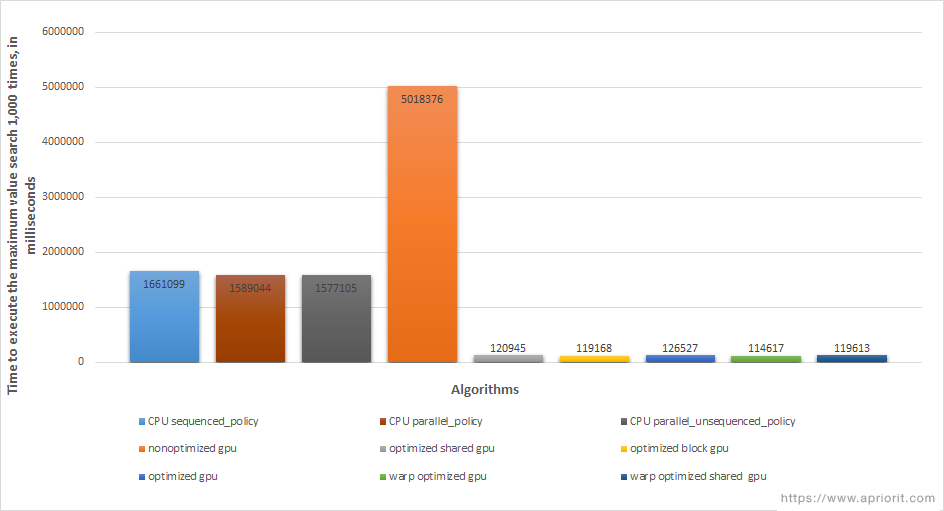
Figure 2. Maximum value search speed using CPU and GPU

The columns in the diagram show the algorithm execution time in milliseconds. The first three columns from the left show execution times on the CPU. The fourth represents the time for linear execution on the GPU, without optimization. As you can see, single-threaded execution on the GPU didn’t lead to any acceleration of computations.

In contrast, the following five columns represent execution times for optimized algorithms on the GPU. All these columns reveal that CUDA acceleration brings impressive results.  

However, there was no significant difference in speed among the optimized algorithms when processing our selected input data. Even the method with warp acceleration didn’t bring the expected boost in speed.

Conclusion

In this article, we compared execution times for algorithms to find the maximum value of an element in a range and its index. Our purpose was to understand CUDA’s GPU acceleration capabilities. In our tests, we saw no significant difference in execution times for algorithms optimized for the GPU. So we can conclude that it would be better to choose an algorithm for executing linear tasks based on parameters other than computation speed: flexibility of configuring graphics systems, complexity of the input data structure, etc. 

 Working with CUDA can provide an enormous increase in computational speed of the GPU, but it also requires deep knowledge of C++ programming. Apriorit has a team of dedicated kernel developers and C++ programmers who have extensive experience working on complicated projects. If you have a challenging project in mind, feel free to contact us.